Fibonacci Sequence

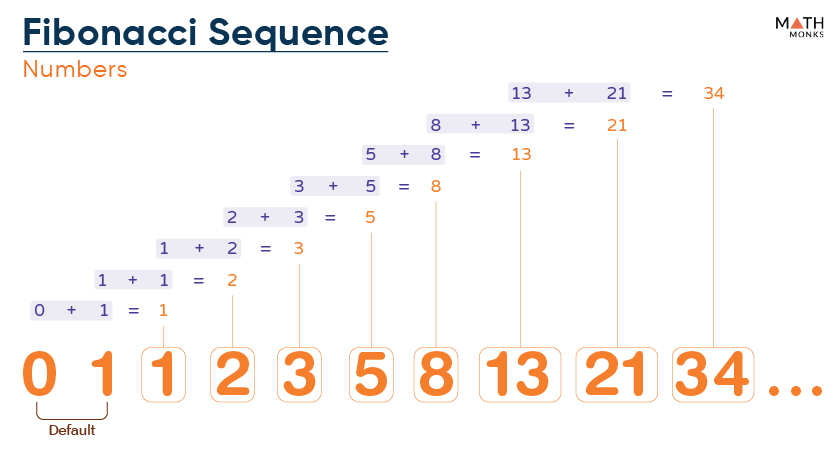
The Fibonacci Sequence is a number series in which each number is obtained by adding its two preceding numbers. It starts with 0 and is followed by 1. The numbers in this sequence, known as the Fibonacci numbers, are denoted by F_n.

The first few numbers of the Fibonacci Sequence are as follows.

Formula

The above sequence can be written as a ‘Rule’, which is expressed with the following equation.

Using this equation, we can conclude that the sequence continues to infinity.

The following table lists each term and term value in the Fibonacci Sequence till the 10 th .

Patterns

The numbers in the sequence follow some interesting patterns:

• Every third number in the series, starting at 2, is a multiple of 2. Similarly, every fourth number after 3 is a multiple of 3, every fifth number after 5 is a multiple of 5, and so on.
• Also, the sum of two odd numbers is always an even number, whereas the sum of an even and an odd number is an odd number. Thus, the Fibonacci sequence follows an even, odd, odd, even, odd, odd pattern.

Recursive Formula in Fibonacci Sequence

Since the Fibonacci sequence is formed by adding the previous two Fibonacci numbers, it is recursive in nature.

To calculate the 50 th term, we need the sum of the 48 th and 49 th terms.

Geometrically, the sequence forms a spiral pattern. It starts with a small square, followed by a larger one adjacent to the first square. It is followed by the sum of the two previous squares, where each square fits into the next one, showing a spiral pattern expanding up to infinity.

The following graph represents it.

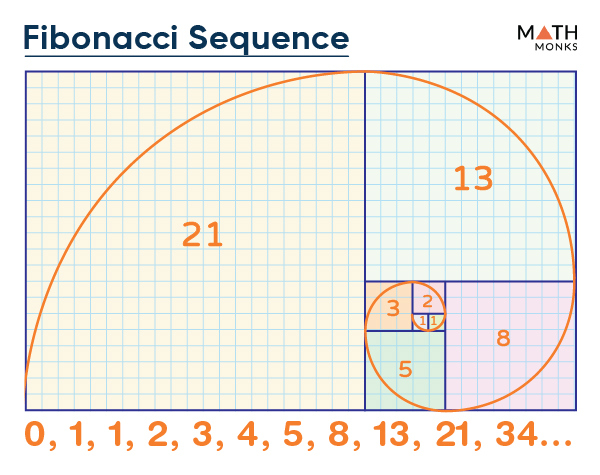
The limits of the squares of all the consecutive Fibonacci numbers create the Fibonacci Spiral.

The Fibonacci Sequence has some important properties, which we will discuss below.

Fibonacci Sequence and Golden Ratio

Two successive Fibonacci numbers give the value $<\phi =\dfrac<1+\sqrt<5>>>$ or, 1.618…, which is known as the Golden Ratio, also known as phi (an irrational number).

For the given spiral, the Golden ratio follows the property:

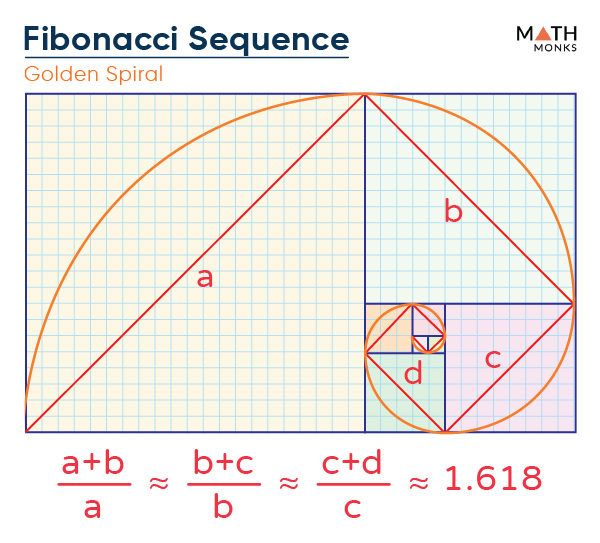
It follows a constant angle close to the Golden Ratio and is commonly known as the Golden Spiral. In geometry, this ratio forms a Golden rectangle, a rectangle whose ratio of its length and breadth gives the Golden Ratio. It appears in many works of art and architecture.

Fibonacci Sequence and Binet’s Formula

Using the Golden Ratio, we can approximately calculate any Fibonacci numbers as

This is known as Binet’s Formula.

The Sum of the Fibonacci Sequence

The sum of the Fibonacci Sequence is obtained by:

where Fn is the nth Fibonacci number, and the sequence starts from F₀.

The sum of the first 12 terms = (12+2) th term – 2 nd term

= 14 th term – 2 nd term

Finding Lucas Numbers from the Fibonacci Sequence

We get another number sequence from the Fibonacci Sequence that follows the same rule mathematically.

Here, the number sequence starting from 2 is formed by adding two preceding numbers, known as Lucas numbers.

The sequence is as follows:

2, 1, 3, 4, 7, ….

Thus, the Lucas numbers are found to get closer to the powers of the Golden Ratio.

Fibonacci Sequence in Pascal’s Triangle

We can also derive the sequence in Pascal’s triangle from the Fibonacci Sequence. It is a number triangle that starts with 1 at the top, and each row has 1 at its two ends. Here, the middle numbers of each row are the sum of the two numbers above it.

Fibonacci Sequence in Real-Life

In Nature

We find the Fibonacci Sequence in various fields, from nature to the human body.

• It appears in plants with many seed heads, pinecones, fruits, and vegetables. The pattern of seeds in the sunflower also follows this sequence.
• We can find this sequence in rabbits. In a pair of a male and a female rabbit, if no rabbits die or leave the place, it forms the Fibonacci sequence 1,1,2,3,5, and so on due to their reproduction.
• The spiral can be seen in seashells and the shapes of snails.
• People claim this is ‘nature’s secret code’ for building the structures perfectly, just like the Great Pyramid of Giza.
• It is also found in the galaxy.

Others

• It is used in coding (distributed systems, computer algorithms )
• It is used in stock prices and other financial data.
• It appears in various fields of study, including cryptography and quantum mechanics.
• The golden ratio and the Fibonacci numbers guide design for websites, architecture, and user interfaces.
• It is also found in paintings. One of the most famous examples was painted by Leonardo da Vinci, the Monalisa. The spiral begins from her left wrist and travels to the background of the painting that follows the sequence.

Solved Examples

Find the sum of the first 15 Fibonacci numbers.

As we know,
The sum of the Fibonacci Sequence = $_F_ = F_ – F_>$
= $$, where F_n is the nth Fibonacci number, and the sequence starts from F₀.
Thus, the sum of the first 15 Fibonacci numbers = (15+2) th term – 2 nd term
= 17 th term – 1
= 987 – 1
= 986

Find the 5 th Fibonacci number.

As we know,
The n th Fibonacci number is F(x_n ) = F(x_n-1) + F(x_n-2), for n>2
Then the 5 th Fibonacci number is F(x₅ ) = F(x_5-1) + F(x_5-2), for n=5
= F(x₄) + F(x₃)
= 2 + 1
= 3

Find the next number when F₁₄ = 377.

Here,
F₁₅ = F₁₄ x Golden ratio
= 377 x 1.618034 (up to 4 decimals)
= 609.9988 (up to 4 decimals), which is approximately 610
Hence, F₁₅ = 610

Calculate the value of F_-6.